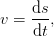
For some reason I keep confusing myself with the units in beat space and the definition of an acceleration in reciprocal time only. How’s that with the usual motion over distance s during time t?
The speed is
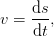 | (1) |
while the acceleration is given as speed increase per covered distance,
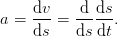 | (2) |
This definition allows to compute the speed after a certain covered distance,
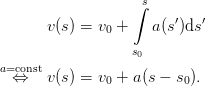 | (3) |
That can be again regarded as a differential equation linking space and time increments, to be solved for the time difference corresponding to two points in space,
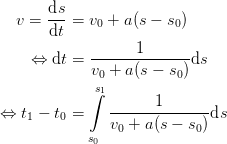 | (4) |
…substituting 3 …
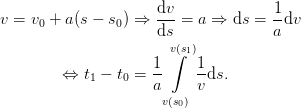 | (5) |
Hence, the duration of a certain distance interval in time is given by
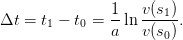 | (6) |
How should one interpret the dimension of the acceleration? The unit s-1 could be seen as (m/s) / m, h-1 as (km/h) / km. One mixed variant could be (km/h) / m, which boils down to 1000 h-1.
The analogy can be carried forward, identifying the distance s with the position in the score, counted in bars, beats, whatever you like. A sensible unit might be a whole note, denoted with the unit symbol n. A quarter note equals Δsnote = 1/4n, an eigth 1/8n. A bar in 6/8 meter has length Δsbar = 3/4n, while in 4/4 meter it’s an unsurprising Δsbar = 1n.
Dominic explained the meaning of the acceleration parameter c as such: After c bars, the tempo increased by 1 bpm. The tempo is always related to quarter notes, so that one bar of three quarters length at constant tempo v = 120bpm, be it either in 3∕4 or in 6∕8 meter, takes 1.5 s to complete. With the bar length
The acceleration value, based on quarter beats per minute, is given by
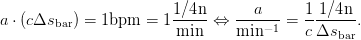 | (7) |
The tempo v(s) at a certain point into the score is given by 3 using this acceleration. Also, a time interval for a certain beat can be computed using 6 and the tempo values at the beginning of the converned beat (s0) and the beginning of the next one (s1).
It is evident from 6 that all this is only applicable if there indeed is a non-zero acceleration a and the tempo is always non-zero. The latter point is illustrative in the spacetime analogy with the conventional definition of a constant acceleration per time interval,
| a | = 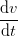 = = 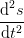 , , | (8) |
Negative acceleration is of course allowed, as long as it is non-zero. For constant tempo, the trivial
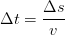 | (9) |
applies.
Actually, the usual notion inside a score is to change tempo from v0 to v1 within a certain number of bars. In place of 7, the acceleration then simply is given by the ratio of the tempo difference and the corresponding distance in the score,
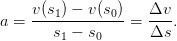 | (10) |
This the obvious sensible default to use when a part length in bars is given without acceleration.
To compare with Dominic’s empirical mean tempo for a beat,
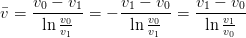 | (11) |
(written to avoid direct logarithms of quantities with units attached), the acceleration in 6 can be replaced by 10. This yields
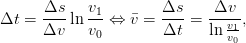 | (12) |
which is the same as Dominic’s expression.
One could also define the metronome tempo acceleration in terms of time. Instead of being given in units of inverse time, it would be beats-per-minute per minute. But how easy is it to solve for the length of a beat Δs then?
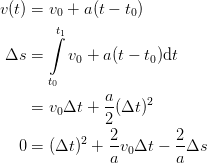 | (13) |
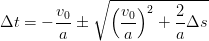 | (14) |
This is straightfoward, allowing for the choice of the positive Δt. Now, what is desired? Constant acceleration in space (beat count) or in time?